Kush ka durim pret më pak
Viktor Ahmeti.5 days ago
Para disa vitesh, teksa ecja në trotuar krahas kolonës së pafund të kerreve luksoze, prej zapullimit të verës dhe ajrit të pastër të Gjilanit, mua më kapi etja dhe u ndala në një dyqan të blej një shishe ujë. Duke u afru tek arka, menjëherë pas personit që sapo pagoi për një Marlboro t’kuqe, e pashë një çift me dy karroca të stërmbushura të cilëve sapo i erdhi rendi për të paguar. Mendova se kur të më shohin mua të gjorin me atë shishe të vetme në dorë nuk do të kishte nevojë as të bëja pyetjen sepse do më lëshonin rendin menjëherë – jo se e kanë obligim por vetëm si akt njëzor. Atyre as që ju shkoi mendja, e edhe kur i pyeta më thanë vrazhdë se “në Gjermani duhet të respektosh rendin” ku dhe u binda për paragjykimet e mija. Kurgjo kërkujt, unë prita disa minuta derisa më erdhi rendi dhe vazhdova ditën time.
Mu kujtua ky rast jo se më mbeti hatri por sepse po më dhimbseshin ato minutat e mi të çuar dëm. Sepse po ta bësh hesap ata pritën 0 minuta, unë prita 10 minuta deri sa paguan ata, pra totali i pritjes sonë ishte 10 minuta. Por po të ma kishin lëshuar rendin unë do prisja 0 minuta, ata do prisnin 30 sekonda deri të paguaja unë, pra totali i pritjes sonë do të ishte 30 sekonda. Vërehet se kohë e vlefshme do të mund të kursehej. Kohë e qytetarëve të Republikës së Kosovës. Kohë që do mund të shpenzohej o për të shtuar vlerë o për të bërë gjithçka tjetër që bëjmë ne Shqiptarët.
Matematika
Ma merr mendja se kjo që spjegova më lart është vetëm një rast special për n=2, e një vërtetim gjeneral mund të bëjmë kur rendi që pret tek arka përbëhet prej n personave. Pyetjen mund ta shtrojmë si më poshtë:
Tek arka, n persona presin në rend për të paguar për sendet e tyre. Si mund ti rendisim ata ashtu që koha totale që shpenzohet duke pritur të minimizohet?
Nëse përgjigja juaj është më shumë arka, self checkout, porosit online, ose ndonjë budallallëk i ngjashëm, nuk jeni të mikpritur <3
Me aftësitë e mija të diskutueshme të matematikës së shkollës së mesme mund të gjejmë përgjigjen. Le të jenë personat në një renditje të rastësishme dhe le të t’i referohemi atyre me numra 1, 2, 3, \ldots sipas renditjes. Kohën që personi i e shpenzon deri sa të përfundon pagesën ta quajmë t_i. Tani mund të llogarisim kohën e pritjes për secilin person:
| Personi 1 | t_1 |
| Personi 2 | t_1+t_2 |
| \ldots | \ldots |
| Personi \text{n-1} | t_1 + t_2 + \ldots + t_{n-2} + t_{n-1} |
| Personi \text{n} | t_1 + t_2 + \ldots + t_{n-2} + t_{n-1} + t_{n} |
Duke i mbledhur pritjet llogarisim që koha totale që shpenzohet është:
M = t_{n} + 2t_{n-1} + \ldots + (n-1)t_2 + nt_1Kur ne i ri-rendisim personat, matematikisht jemi duke i ri-renditur vlerat t_i, pra mjafton të gjejmë renditjen optimale të t_i që vlera M të minimizohet. Tërë kjo ri-renditje sjell në mend Pabarazimin e Rirenditjes, të cilin mund ta aplikojmë direkt këtu.
Qartazi kemi 1 \leq 2 \leq \ldots \leq n. Andaj prej Pabarazimit të Rirenditjes kemi se vlera M arrin maksimumin kur t_{n} \geq t_{n-1} \geq \ldots \geq t_1, pra kur anëtarin më të vogël të vargut të parë e shumëzojmë me anëtarin më të madh të vargut të dytë e kështu me rradhë. Po e përkthyem në gjuhën shqipe do të thotë se personi i parë duhet të ketë më së pakti gjësende, i dyti më shumë se ai, e kështu me rradhë deri tek çifti Gjerman të cilët duhet të qëndrojnë të fundit me dy karrocat e tyre gjigante.
Pra u gjet përgjigja: gjithmonë duhet ti lëshojmë rendin të gjithë personave që kanë më pak gjësende për të paguar sesa ne. Në këtë mënyrë koha e shpenzuar duke pritur minimizohet dhe të gjithë fitojmë. Ah, po të ishte jeta kaq e thjeshtë. Puna është që njerëzve nuk ju intereson gjithmonë aq shumë e mira e grupit sa ju intereson e mira e vet. Prapseprapë, po supozuam se njerëzit kanë tendencë të blejnë në vendet e njejta, e gjatë vizitave të shpeshta herë do blejnë shumë e herë pak, herë do qëllojnë në ditë të ngarkuara e herë të zbrazëta, atëherë ndoshta pahiri do ju shkojë mendja të lëshojnë rendin sepse në të ardhmen dikush do i’a lëshojë rendin edhe atyre.
Kompjuteri
Unë nuk mund të shkoj më larg se aq me matematikë, e besa me rezultat nuk jam i kënaqur – thjeshtë realiteti është më i komplikuar. Sipas përgjigjes optimale që gjetëm më lart, personit me më së shumti artikuj në një ditë shumë të ngarkuar do ti vijë rendi për të paguar i fundit para se të mbyllet dyqani. Të shohim se a do mund të gjejmë ndonjë strategji të thjeshtë ku pritja maksimale nuk teprohet, por edhe ku si grup koha e pritjes i afrohet minimales.
Së pari duhet ti gjenerojmë disa bashkësi të dhënash që reprezentojnë njerëzit që vijnë tek arka. Për të bërë gjërat më të thjeshta, kohën e ndajmë në time steps (ts) ku një produkt skanohet për 1ts. Në çdo time step ose nuk ndodh asgjë ose vjen një person i ri me një numër të caktuar të produkteve. Pra datasetet do të duken sikur “0, 0, 3, 0, 7, 0, 0, 0, 22, 0, …” e kështu me rradhë. Do të gjenerojmë 100 datasete me nga 500ts, ku përafërsisht 50 persona vijnë tek arka. Pra, në çdo moment, ekziston gjasa 10% që një person i ri të vijë.
Bukur, tani duhet të modelojmë numrin e produkteve që njerëzit i blejnë. Edhe kjo ndoshta është pak subjektive, mirëpo sipas përvojës sime shumica e njerëzve kanë pak produkte e një pakicë ka më shumë. Pra na duhet një shpërndarje jo normale, por e anuar nga e majta dhe me bisht të zgjatur të hollë. Besoj me vizatim kuptohet më mirë:
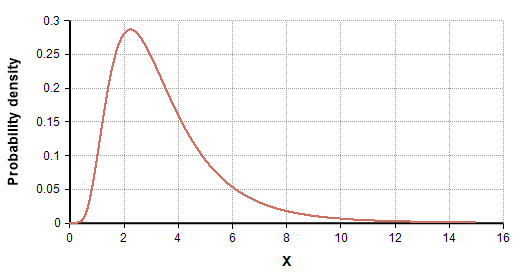
Pasi kombinova inteligjencën time natyrale dhe atë të mikut tim me intelegjencë artificiale, vendosëm të përdorim shpërndarjen Shifted Negative Binomial e cila duket shumë e ngjashme me Log Normal por përshtatet më shumë për rastin tonë. Me pak Python mund ti gjenerojmë pa problem datasetet.
Tani për simulim i definojmë dy klasa të rëndësishme:
# Reprezenton një person që pret në rend
@dataclass
class Person:
num_groceries: int
wait_time: int = 0
# Reprezenton rezultatin e një simulimi
@dataclass
class Stats:
wait_times: List[int] = field(default_factory=list)
max_queue: int = 0
@property
def total_customers(self) -> int:
return len(self.wait_times)
@property
def total_wait_time(self) -> int:
return sum(self.wait_times)
@property
def max_wait_time(self) -> int:
return max(self.wait_times, default=0)
@property
def avg_wait_time(self) -> float:
return self.total_wait_time / self.total_customers if self.total_customers else 0.0Këto definime pastaj mund ti shfrytëzojmë kur bëjmë simulimin në një dataset. Në çdo time_step, nëse vjen një person i ri atëherë ai vendoset në pozitën e tij finale në rend (varësisht prej strategjisë që zgjedhim), kurse personit të parë në rend ia zvogëlojmë shportën për 1 ose e largojmë nga lista. Pas konsiderimit të disa detajeve vijmë tek ky kod (jo më i bukuri në botë):
def run_simulation(data, strategy):
stats = Stats()
queue = deque() # Përdorim deque për largime të shpejta prej fillimit të listës
time_step = -1
while True:
time_step += 1
if time_step < len(data) and data[time_step] > 0:
queue.append(Person(num_groceries=data[time_step]))
strategy(queue)
stats.max_queue = max(stats.max_queue, len(queue))
for person in list(queue)[1:]:
person.wait_time += 1
if not queue:
if time_step >= len(data):
break
continue
front = queue[0]
if front.num_groceries == 0:
finished = queue.popleft()
stats.wait_times.append(finished.wait_time)
else:
front.num_groceries -= 1
return statsShohim se ky funksion merr si parametër strategy i cili është një funksion që vendos personin e ri në vendin e duhur sipas një strategjie të caktuar. Strategjia më e thjeshtë është ajo vetjake e cila nuk lejon askënd të kalojë:
def selfish(queue: Deque[Person]) -> None:
"""Never allow passing."""
returnStrategjia tjetër është ajo matematikisht optimale e cila e lejon gjithmonë personin me më pak gjësende të kalojë:
def optimal(queue: Deque[Person]) -> None:
"""Let people with fewer groceries pass."""
curr = len(queue) - 1
groceries = queue[curr].num_groceries
i = curr - 1
while i > 0 and groceries < queue[i].num_groceries:
curr = i
i -= 1
queue.insert(curr, queue.pop())Sa për test, do përfshijmë strategjinë random e cila 50% të kohës i lejon njerëzit të kalojnë:
def sometimes(queue: Deque[Person]) -> None:
"""Probabilistic passing."""
curr = len(queue) - 1
groceries = queue[curr].num_groceries
i = curr - 1
while i > 0:
if random.random() < 0.5:
curr = i
i -= 1
else:
break
queue.insert(curr, queue.pop())Të shohim se si mund të shfaqim vizualisht rezultatet që ti analizojmë. Më e thjeshta është të shfaqim pritjen e personave nëpër të gjithë datasetin:
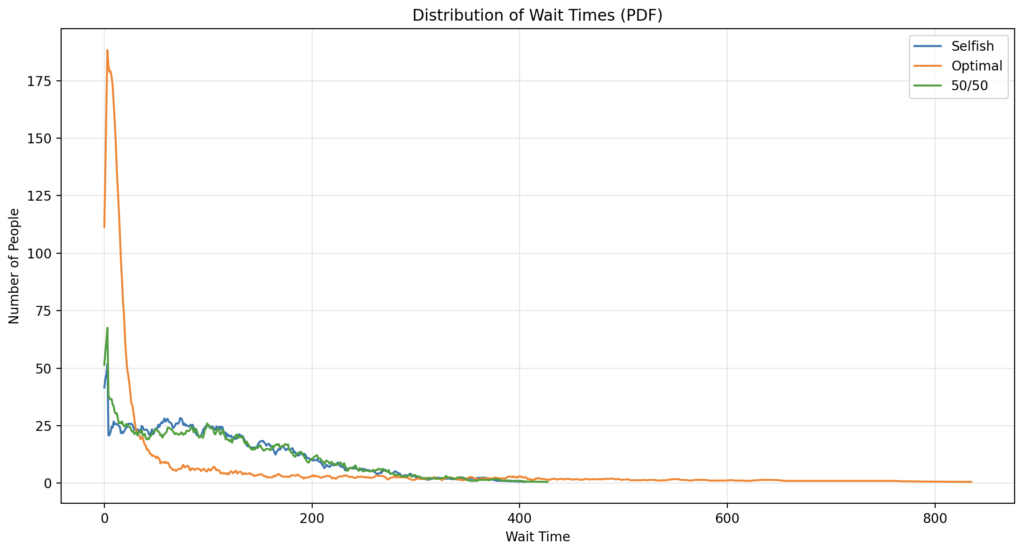
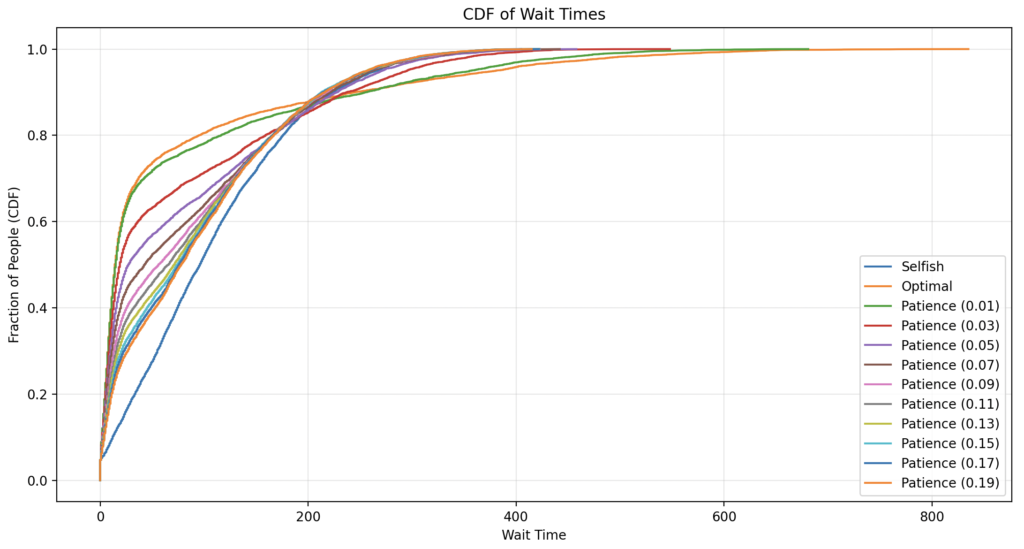
Shohim se strategjia vetjake është relativisht mirë e shpërndarë por shumë njerëz presin. Strategjia 50/50 nuk sjell kurrfarë përfitimi. Strategjia optimale lejon një numër shumë të madh të njerëzve të presin shumë pak (ana e majtë) por pak njerëz presin jashtëzakonisht shumë (bishti tejet i zgjatur në anën e djathtë). Pamje edhe më e qartë na del kur vizualizojmë shpërndarjen kumulative, pra përqindjen e njerëzve që presin më pak se një kohë e caktuar:
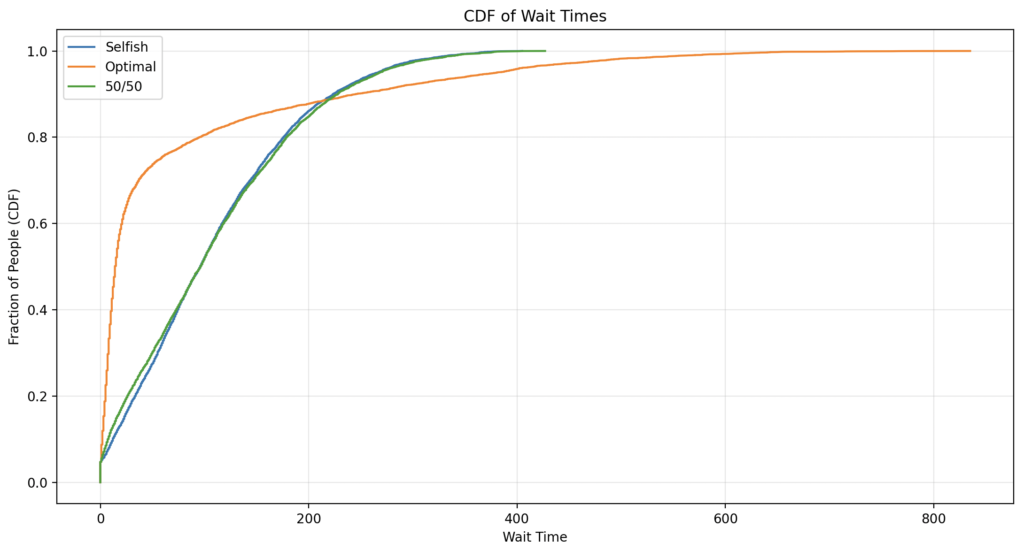
Tani po shohim vizualisht problemin praktik: Mesatarja e pritjes po zvogëlohet por pritja më e gjatë është shumë e gjatë. A do mund të gjejmë një strategji më konvekse se strategjia vetjake por me bisht përafërsisht të gjatë sa ajo? Unë mendova gjerë e gjatë për këtë dhe erdha te një zgjidhje e thjeshtë, ta quajmë strategjia M: të veprojmë sipas strategjisë optimale por të kemi një cutoff, pra një numër maksimal të njerëzve që mund të na kalojnë. Pas simulimit me cutoffs 3, 5, 7, 10, 15 kemi këtë rezultat:
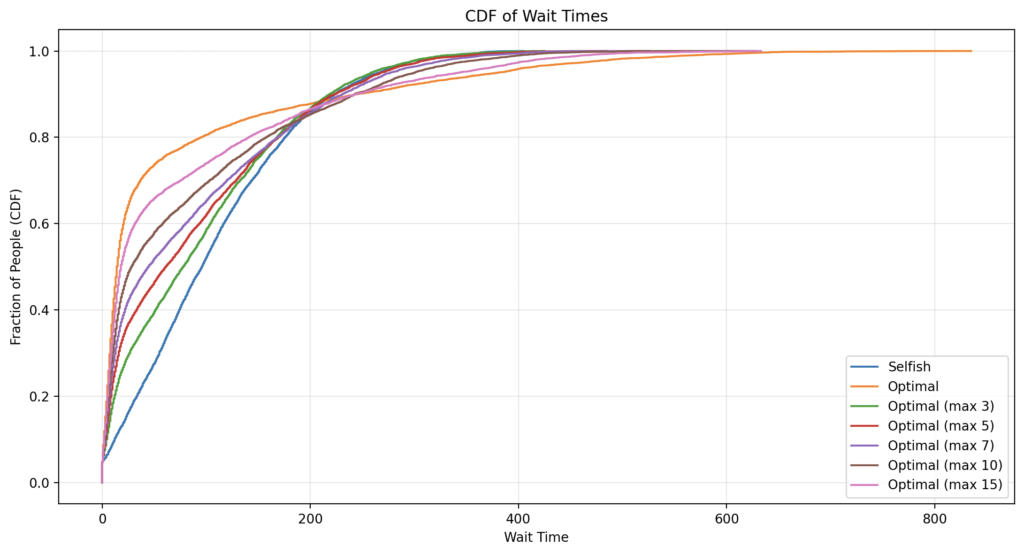
Çka është interesant është se sa më i madh cutoff, aq më konveks funksioni (më e vogël mesatarja) por edhe aq më i gjatë bishti. Duhet të jetë subjektive zgjedhja se cili funksion nga famija M është “më i mirë” varësisht se sa të durueshëm janë njerëzit. Si funksion është i thjeshtë sepse njerëzit mund ta mbajnë lehtë në mend strategjinë, por mund ta definojmë edhe më saktë këtë cutoff.
Pas një bisede me makiato me mikun tim Leart Ajvazaj, ai ma dha një strategji më rigoroze, ta quajmë strategjia P: për çdo person që na kalon, numrin e gjësendeve e shumëzojmë me një numër në intervalin (0,1) dhe, në mendjen tonë, e llogarisim se kemi po aq gjësende. Shqip, mund ta mendojmë se secili person ka aq durim sa ka gjësende, dhe dalngadalë i humb durimi, dhe ri-renditja bëhet duke krahasuar durimet e njerëzve. Varësisht prej konstantës që zgjedhim në (0,1) kemi strategjitë në vijim:
Në të dy rastet duhet të zgjedhim nga një konstante që të definojmë saktë strategjinë, por në përgjithësi po duket se strategjia e dytë është “më e mirë” se e para, sepse durimi varet prej numrit të gjësendeve, kurse në strategjinë e parë zgjdedhim maksimumin në mënyrë naive. Tani le ti krahasojmë ato me një vizualizim interesante.
Problemi jonë ka dy objektiva: të minimizojë mesataren dhe të kufizojë maksimumin e pritjes. Nëse i marrim këta dy parametra parasysh, atëherë mund ti vendosim strategjitë në një rrafsh dhe të krijojmë një Pareto Frontier, ku strategjitë dominuese na dalin në kufi. Ja vizualizimi:
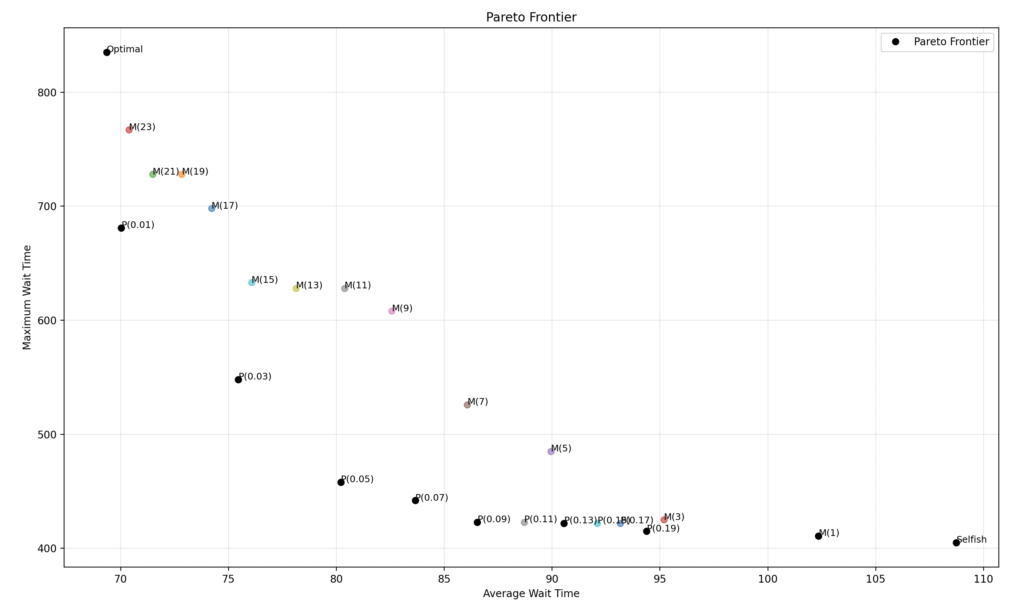
Strategjia optimale është majtas lart (mesatare të vogël, maksimum të madh) kurse strategjia vetjake është djathtas poshtë (mesatare e madhe, maksimum i madh). Strategjitë e tjera janë midis tyre. Pareto Frontier janë pikat e zeza në kufirin e poshtëm, dhe jo çuditërisht janë të gjitha strategji P, që vërteton që strategjitë P janë objektivisht më të mira se ato M. Në këtë rast strategjia P(0.03) duket shumë e mirë.
Për të parë edhe më saktë këtë vizualizim, le të zëvendësojmë pritjen maksimale me pritjen 99th percentile e cila është mjaftueshëm reprezentative dhe nuk është e ndjeshme nga vlerat ekstreme. Tani vizualizimi duket edhe më bukur:
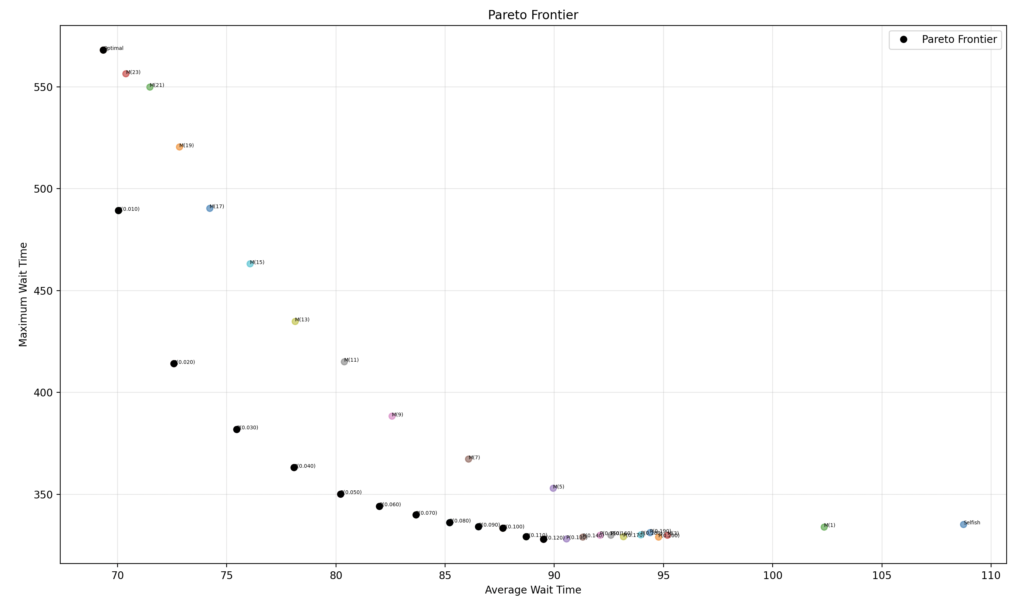
Unë jam shumë i kënaqur me strategjitë P, vetëm se mund të jetë vështirë për mua dhe për çiftin Gjerman ti bëjmë këto llogaritje në kokë. Por nëse jemi të durueshëm dhe na humb durimi njejtë në proporcion me numrin e gjësendeve që kemi për ti paguar, besoj do ia dalim përafërsisht.
Hulumtim 5 minutësh
Jo aq çuditërisht, njerzëzit veq se kanë menduar për këtë problem para meje në një fushë të quajtur Queuing Theory. Normalisht që ne po punojmë me një rriskë të kësaj fushe, ku dihet koha për procesimin e një elementi në rend, ri-renditjen nuk e llogaritim që merr kohë, e kështu me rradhë.
Për rastin tonë, zgjidhja optimale qenka saktë Shortest Job Next që e minimizon pritjen mesatare. Paskan vërejtur se kjo lë proceset e gjata në pritje andaj ekzistoka Highest Response Ratio Next, që dalngadalë zvogëlon durimin e elementeve në rend. Shumë çuditërisht, unë e implementova atë në datasetin tim dhe rezultati doli i ngjashëm me strategjitë M por shumë larg Pareto Frontier. Çka do të thotë kjo? Se di por nuk besoj se bëmë ndonjë zbulim.
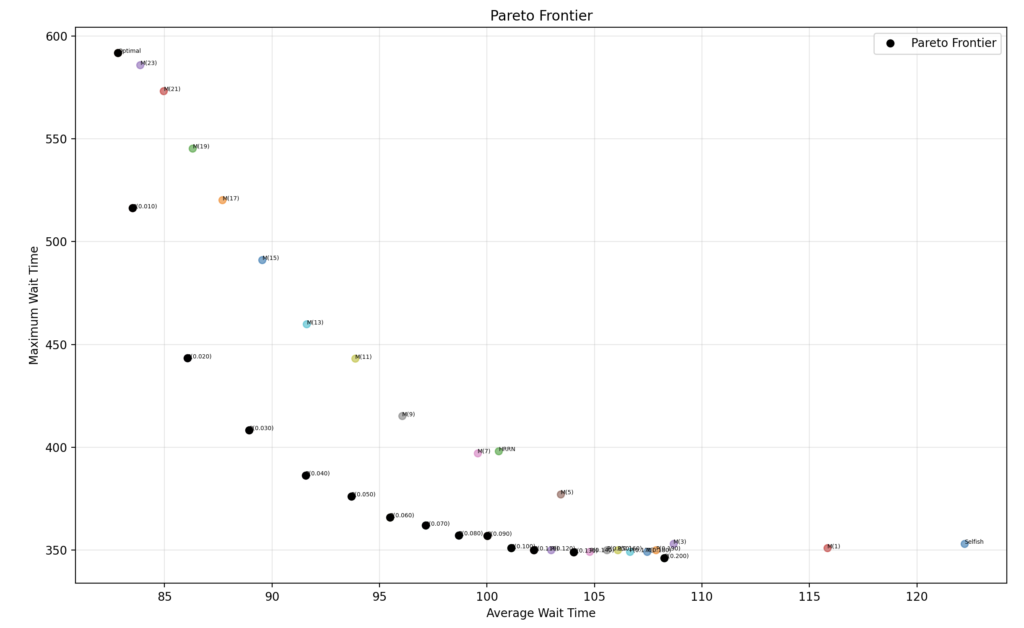
Pyetje të tjera për ti eksploruar (bashkë me mendimet e mija):
- A ekziston ndonjë strategji që i afrohet edhe më shumë pikës majtas poshtë (në Pareto Frontier)? – Besoj se po
- A mund të optimizojmë një rrjetë neurale që të krijojë një strategji të mirë? – Besoj se po
- A mund të gjejmë strategji evolucionarisht stabile? – Vështirë të definohen kushtet
- Çfarë strategji të reja ekzistojnë në rast se kemi dy arka paralele? – Arkë e veçantë për personat me shumë produkte?
Përmbyllje
Inspirimi im ishte tek arka, por temat që i diskutova mund të aplikohen në çdo sistem ku ka gjëra për tu procesuar në varg dhe ska hapsirë për zgjerim horizontal. E pasi nuk qenka aq e lehtë ti prioritizojmë gjërat, sepse objektivi nuk është i vetëm, mendoj se instikti jonë është të aplikojmë gjithnjë strategjinë optimale – ti përfundojmë gjërat e lehta në fillim e të vështirat kurrë. Në mend më shkojnë tiketat e paprioritizuara të bugs në Jira që mbesin pa u kryer për vite të tëra, apo ato librat e gjatë e të vështirë që i mbulon pluhuri në raft e mbesin me vite të palexuar.
← All blogs